Главная Ходовая часть

§1.18. графики зависимости модуля и проекции ускорения и модуля и проекции скорости от времени при движении с постоянным ускорением

Графики дают возможность представить зависимость скорости и ускорения от времени при движении тела (точки) наглядно.
Графики модуля и проекции ускорения
Если точка движется с постоянным ускорением, то графики модуля и проекции ускорения будут прямыми, параллельными оси времени. Надо помнить, что модуль - неотрицательная величина, поэтому график модуля ускорения не может быть расположен ниже оси времени (рис. 1.50). Проекции ускорения могут иметь положительные и отрицательные значения (рис. 1.51, а, б). Рисунок 1.51, б показывает, что ускорение постоянно и направлено противоположно оси X.
Рис. 1.50

о
По графику проекции ускорения можно найти, кроме ах, изменение проекции скорости. Оно численно равно площади пря-моугольника ОАВС или OKMN, так как Avx = axt, a axt численно равно площади прямоугольника ОАВС или OKMN.
Площадь берется со знаком минус, если она расположена ниже оси времени, что соответствует рисунку 1.51, б, где Avx = axt
Формулы проекций скорости (1.17.3) являются линейными функциями времени. Поэтому графики модуля и проекций ско-рости представляют собой прямые линии. На рисунке 1.52 пред-ставлены графики зависимости модуля скорости от времени для трех движений с постоянным ускорением. Графики 2 и 3 соот-ветствуют движениям, модули начальных скоростей которых соответствуют отрезкам OA и ОБ. График 1 соответствует движению с равномерно возрастающим модулем скорости и начальной скоростью, равной нулю. График 3 соответствует движению с модулем скорости, равномерно убывающим до ну-ля. Отрезок ОС численно равен времени движения точки до ос-тановки. Рис. 1.52
График проекции скорости
Графики модуля скорости содер- /1
о
жат меньше информации, чем графики проекции скорости, так как по первым графикам нельзя судить о направлении движения относительно координатных осей.
Рис. 1.53
На рисунке 1.53 изображены графики 1, 2 проекций скорости двух точек. Обе они имеют начальную скорость, равную нулю. Первая точка движется в
положительном направлении оси X, и так как Avx > 0, то а1х > 0. Вторая точка движется противоположно оси X, так как Avx На рисунке 1.54 также изображены графики 1, 2 проекций скорости двух точек. Обе они имеют одно и то же значение проекции начальной скорости, соответствующее отрезку OA. Согласно графику 1 точка движется в положительном направлении оси X, причем модуль и проекция скорости равномерно возрастают.
Согласно графику 2 (см. рис. 1.54) точка в течение некоторого промежутка времени (отрезок ОВ) движется в положительном направлении оси X (vx > 0) с равномерно уменьшающимся до нуля (остановка) значением проекции скорости. После этого проекция скорости становится отрицательной; это означает, что точка стала двигаться в направлении, противоположном положительному направлению оси X. При этом проекция скорости по модулю, а значит, и модуль скорости равномерно увеличиваются. Проекция ускорения точки отрицательна. Так как проекция скорости точки равномерно убывает, то проекция ускорения остается постоянной. Следовательно, точка движется с постоянным ускорением.
Графики зависимости скорости и ускорения от времени при постоянном ускорении довольно просты. Глав-ное здесь - привыкнуть к изображению положительных и отрицательных величин и не путать графики модулей и проекций.
? 1. Покажите, что угол наклона графика проекции скорости к оси времени тем больше, чем больше модуль проекции ускорения, т. е. проекция ускорения является угловым коэффициентом прямой.
2. На рисунке 1.55 изображены графики 1, 2 проекций скорости двух точек. Докажите, что графики соответствуют движению с ускорением, не изменяющимся как по модулю, так и по направлению.? Рис. 1.54 Рис. 1.55
Как изменяется скорость точки, график проекции скорости которой в зависимости от времени изображен прямой 1 (см. рис. 1.55)? Чему соответствуют отрезки ОС и ОХ>?
Как изменялась скорость точки (см. график 2 на рисунке 1.55)? Чему соответствует отрезок ОС? Куда направлено ускорение точки относительно оси XI

1.2. Прямолинейное движение

1.2.3. Графическое вычисление кинематических величин

Некоторые кинематические характеристики движения можно рассчитать графическим способом.

Определение проекции скорости

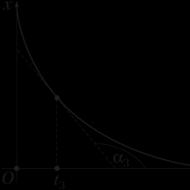
По графикам зависимости координаты от времени x (t ) (или пройденного пути от времени S (t )) можно рассчитать соответствующую проекцию скорости v x в определенный момент времени (рис. 1.11), например t = t 1 .

Для этого следует:

1) отметить на оси времени указанное значение момента времени t 1 ;

2) восстановить перпендикуляр до пересечения с графиком x (t );

5) определить проекцию скорости на ось Ox как тангенс угла наклона касательной к положительному направлению оси времени:

v x (t 1) = tg α 1 .

Следует отметить, что проекция скорости v x является

положительной , если касательная к графику образует острый угол с направлением оси t (см. рис. 1.11);
отрицательной , если касательная к графику образует тупой угол с направлением оси t (рис. 1.12).

На рис. 1.12 изображен график зависимости координаты от времени x (t ). Для определения проекции скорости на ось Ox в момент времени t 3 проведен перпендикуляр t = t 3 . В точке пересечения перпендикуляра с зависимостью x (t ) проведена касательная линия. Она образует тупой угол с осью t . Следовательно, проекция скорости v x на ось Ox в указанный момент времени является отрицательной величиной:

v x (t 3) = − | tg α 3 | .

Рис. 1.12

Определение проекции ускорения

По графику зависимости проекции скорости от времени v x (t ) можно рассчитать проекцию ускорения a x на соответствующую ось в определенный момент времени (рис. 1.13), например t = t 2 .

Для этого следует:

1) отметить на оси времени указанное значение момента времени t 2 ;

2) восстановить перпендикуляр до пересечения с графиком v x (t );

3) провести к графику касательную линию в точке его пересечения с перпендикуляром;

5) определить проекцию ускорения на ось Ox как тангенс угла наклона касательной к положительному направлению оси времени:

a x (t 2) = tg α 2 .

Следует отметить, что проекция ускорения a x является

положительной , если касательная к графику образует острый угол с направлением оси t (см. рис. 1.13);

Рис. 1.13

отрицательной , если касательная к графику образует тупой угол с направлением оси t (рис. 1.14).

Рис. 1.14

Пояснение к использованию алгоритма. На рис. 1.14 изображен график зависимости проекции скорости от времени v x (t ). Для определения проекции ускорения на ось Ox в момент времени t 4 проведен перпендикуляр t = t 4 . В точке пересечения перпендикуляра с зависимостью v x (t ) проведена касательная линия. Она образует тупой угол с осью t . Следовательно, проекция ускорения a x на ось Ox в указанный момент времени является отрицательной величиной:

a x (t 4) = − | tg α 4 | .

Определение пройденного пути и модуля перемещения (комбинация равномерного и равноускоренного движения)

По графику зависимости проекции скорости от времени v x (t ) можно рассчитать пройденный путь и модуль перемещения материальной точки (тела) за определенный промежуток времени ∆t = t 2 − t 1 .

Для расчета указанных характеристик по графику, содержащему участки только равноускоренного и равномерного движения, следует:

4) вычислить пройденный путь S и модуль перемещения ∆r как суммы:

∆r = S 1 + S 2 + ... + S n ,

где S 1 , S 2 , ..., S n - пути, пройденные материальной точкой на каждом из участков равноускоренного и равномерного движения.

На рис. 1.15 показана зависимость проекции скорости от времени для материальной точки (тела), движущейся на участке AB равноускоренно, на участке BC - равномерно, на участке CD - равноускоренно, но с ускорением, отличающимся от ускорения на участке AB .

Рис. 1.15

В этом случае пройденный путь S и модуль перемещения ∆r совпадают и рассчитываются по формулам:

S = S 1 + S 2 + S 3 ,

∆r = S 1 + S 2 + S 3 ,

где S 1 - путь, пройденный материальной точкой (телом) на участке AB ; S 2 - путь, пройденный на участке BC ; S 3 - путь, пройденный на участке CD ; S 1 , S 2 , S 3 рассчитываются по алгоритму, приведенному выше.

Определение пройденного пути и модуля перемещения (комбинация равномерного, равноускоренного и равнозамедленного движения)

Для расчета указанных характеристик по графику v x (t ), содержащему участки не только равноускоренного и равномерного, но и равнозамедленного движения, следует:

1) отметить на оси времени указанный интервал времени ∆t ;

2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком v x (t );

4) вычислить пройденный путь S как сумму:

S = S 1 + S 2 + ... + S n ,

где S 1 , S 2 , ..., S n - пути, пройденные материальной точкой на каждом из участков;

5) вычислить модуль перемещения как разность суммарного пути, пройденного материальной точкой до точки остановки, и пути, пройденного материальной точкой после остановки.

Пояснение к использованию алгоритма . На рис. 1.16 показана зависимость скорости от времени для материальной точки (тела), движущейся на участке AB равноускоренно, на участке BC - равномерно, на участке CF - равнозамедленно.

Рис. 1.16

В том случае, когда есть участок равнозамедленного движения (включающий точку остановки - точка D ), пройденный путь S и модуль перемещения ∆r не совпадают. Пройденный путь вычисляют по формуле

S = S 1 + S 2 + S 3 + S 4 ,

где S 1 - путь, пройденный материальной точкой (телом) на участке AB ; S 2 - путь, пройденный на участке BC ; S 3 - путь, пройденный на участке CD ; S 4 - путь, пройденный на участке DF ; S 1 , S 2 , S 3 , S 4 рассчитываются по алгоритму, приведенному выше; необходимо отметить, что величина S 4 является положительной.

Модуль перемещения вычисляют по формуле

∆r = S 1 + S 2 + S 3 − S 4 ,

вычитая путь, пройденный материальной точкой (телом) после поворота.

Определение модуля изменения скорости

По графику зависимости проекции ускорения от времени a x (t ) можно найти модуль изменения скорости ∆v материальной точки (тела) за определенный интервал времени ∆t = t 2 − t 1 (рис. 1.17).

Для этого следует:

1) отметить на оси времени указанный интервал времени ∆t ;

2) восстановить перпендикуляры из точек t = t 1 и t = t 2 до пересечения с графиком a x (t );

4) вычислить модуль изменения скорости за указанный интервал времени как площадь.

Пример 4. График зависимости проекции скорости первого тела на ось Ox от времени изображается прямой, проходящей через точки (0; 6) и (3; 0), второго - через точки (0; 0) и (8; 4), где скорость задана в метрах в секунду, время - в секундах. Во сколько раз отличаются модули ускорений первого и второго тел?

Решение. Графики зависимости проекций скорости от времени для обоих тел показаны на рисунке.

Проекция ускорения первого тела определяется как тангенс тупого угла α 1 ; ее модуль вычисляем по формуле

| a x 1 | = | tg α 1 | = | tg (180 − α 3) | = 6 3 = 2 м/с 2 .

Первое тело движется равнозамедленно; величина его ускорения составляет a 1 = = 2 м/с 2 .

Проекция ускорения второго тела определяется как тангенс острого угла α 2 ; ее модуль вычисляем по формуле

a x 2 = tg α 2 = 4 8 = 0,5 м/с 2 .

Второе тело движется равноускоренно; величина его ускорения составляет a 2 = 0,5 м/с 2 .

Искомое отношение модулей ускорений первого и второго тел равно:

a 1 a 2 = 2 0,5 = 4 .

Величина ускорения первого тела больше величины ускорения второго тела в 4 раза.

Пример 5. График зависимости y -координаты от времени для первого тела изображается прямой, проходящей через точки (0; 0) и (5; 3), второго - через точки (3; 0) и (6; 6), где координата задана в метрах, время - в секундах. Определить отношение модулей проекций скоростей указанных тел.

Решение. Графики зависимости y -координаты от времени для обоих тел показаны на рисунке.

Проекция скорости первого тела определяется как тангенс угла α 1 ; ее модуль вычисляем по формуле

v y 1 = tg α 1 = 3 5 = 0,6 м/с.

Проекция скорости второго тела определяется как тангенс угла α 2 ; ее модуль вычисляем по формуле

v y 2 = tg α 2 = 6 3 = 2 м/с.

Обе проекции скоростей имеют положительный знак; следовательно, оба тела движутся равноускоренно.

Отношение модулей проекций скоростей указанных тел составляет:

| v y 2 | | v y 1 | = 2 0,6 ≈ 3 .

Величина проекции скорости второго тела больше величины проекции скорости второго тела приблизительно в 3 раза.

Пример 6. График зависимости скорости тела от времени изображается прямой, проходящей через точки (0; 4,0) и (2,5; 0), где скорость задана в метрах в секунду, время - в секундах. Во сколько раз путь, пройденный телом, больше модуля перемещения за 6,0 с движения?

Решение. График зависимости скорости тела от времени показан на рисунке. Точка остановки τ ост = 2,5 с попадает в интервал от 0 с до 6,0 с.

Следовательно, пройденный путь представляет собой сумму

S = S 1 + S 2 ,

а модуль перемещения - разность

| Δ r → | = | S 1 − S 2 | ,

где S 1 - путь, пройденный телом за интервал времени от 0 с до 2,5 с; S 2 - путь, пройденный телом за интервал времени от 2,5 с до 6,0 с.

Значения S 1 и S 2 рассчитаем графически как площади треугольников, показанных на рисунке:

S 1 = 1 2 ⋅ 4,0 ⋅ 2,5 = 5,0 м;

S 2 = 1 2 ⋅ (6,0 − 2,5) ⋅ 5,6 = 9,8 м.

Замечание : значение скорости v = 5,6 м/с в момент времени t = 6,0 c получено из подобия треугольников, т.е. из отношения

v 4,0 = 6,0 − 2,5 2,5 − 0 .

Вычислим пройденный путь:

S = S 1 + S 2 = 5,0 + 9,8 = 14,8 м

и величину перемещения:

| Δ r → | = | S 1 − S 2 | = | 5,0 − 9,8 | = 4,8 м.

Найдем искомое отношение пройденного пути и модуля перемещения:

S | Δ r → | = 14,8 4,8 ≈ 3,1 .

Пройденный путь приблизительно в 3,1 раза превышает величину перемещения.

Равномерное движение - это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение - это движение по прямой линии, то есть траектория прямолинейного движения - это прямая линия.

Это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

Скорость равномерного прямолинейного движения не зависит от времени и в каждой точке траектории направлена также, как и перемещение тела. То есть вектор перемещения совпадает по направлению с вектором скорости. При этом средняя скорость за любой промежуток времени равна мгновенной скорости:

vcp = v

Скорость равномерного прямолинейного движения - это физическая векторная величина, равная отношению перемещения тела за любой промежуток времени к значению этого промежутка t:

= / t

Таким образом, скорость равномерного прямолинейного движения показывает, какое перемещение совершает материальная точка за единицу времени.

Перемещение при равномерном прямолинейном движении определяется формулой:

Пройденный путь при прямолинейном движении равен модулю перемещения. Если положительное направление оси ОХ совпадает с направлением движения, то проекция скорости на ось ОХ равна величине скорости и положительна:

vx = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

s = vt = x - x0

где x 0 - начальная координата тела, х - конечная координата тела (или координата тела в любой момент времени)

Уравнение движения , то есть зависимость координаты тела от времени х = х(t), принимает вид:

х = x0 + vt

Если положительное направление оси ОХ противоположно направлению движения тела, то проекция скорости тела на ось ОХ отрицательна, скорость меньше нуля (v < 0), и тогда уравнение движения принимает вид:

х = x0 - vt

Равномерное прямолинейное движение - это частный случай неравномерного движения.

Неравномерное движение - это движение, при котором тело (материальная точка) за равные промежутки времени совершает неодинаковые перемещения. Например, городской автобус движется неравномерно, так как его движение состоит в основном из разгонов и торможений.

Равнопеременное движение - это движение, при котором скорость тела (материальной точки) за любые равные промежутки времени изменяется одинаково.

Ускорение тела при равнопеременном движении остаётся постоянным по модулю и по направлению (a = const).

Равнопеременное движение может быть равноускоренным или равнозамедленным.

Равноускоренное движение - это движение тела (материальной точки) с положительным ускорением, то есть при таком движении тело разгоняется с неизменным ускорением. В случае равноускоренного движения модуль скорости тела с течением времени возрастает, направление ускорения совпадает с направлением скорости движения.

Равнозамедленное движение - это движение тела (материальной точки) с отрицательным ускорением, то есть при таком движении тело равномерно замедляется. При равнозамедленном движении векторы скорости и ускорения противоположны, а модуль скорости с течением времени уменьшается.

В механике любое прямолинейное движение является ускоренным, поэтому замедленное движение отличается от ускоренного лишь знаком проекции вектора ускорения на выбранную ось системы координат.

Средняя скорость переменного движения определяется путём деления перемещения тела на время, в течение которого это перемещение было совершено. Единица измерения средней скорости - м/с.

vcp = s / t

Это скорость тела (материальной точки) в данный момент времени или в данной точке траектории, то есть предел, к которому стремится средняя скорость при бесконечном уменьшении промежутка времени Δt:

Вектор мгновенной скорости равнопеременного движения можно найти как первую производную от вектора перемещения по времени:

= "

Проекция вектора скорости на ось ОХ:

vx = x’

это производная от координаты по времени (аналогично получают проекции вектора скорости на другие координатные оси).

Это величина, которая определяет быстроту изменения скорости тела, то есть предел, к которому стремится изменение скорости при бесконечном уменьшении промежутка времени Δt:

Вектор ускорения равнопеременного движения можно найти как первую производную от вектора скорости по времени или как вторую производную от вектора перемещения по времени:

= " = " Учитывая, что 0 - скорость тела в начальный момент времени (начальная скорость), - скорость тела в данный момент времени (конечная скорость), t - промежуток времени, в течение которого произошло изменение скорости, будет следующей:

Отсюда формула скорости равнопеременного движения в любой момент времени:

0 + t Если тело движется прямолинейно вдоль оси ОХ прямолинейной декартовой системы координат, совпадающей по направлению с траекторией тела, то проекция вектора скорости на эту ось определяется формулой:

vx = v0x ± axt

Знак «-» (минус) перед проекцией вектора ускорения относится к равнозамедленному движению. Аналогично записываются уравнения проекций вектора скорости на другие оси координат.

Так как при равнопеременном движении ускорение является постоянным (a = const), то график ускорения - это прямая, параллельная оси 0t (оси времени, рис. 1.15).

Рис. 1.15. Зависимость ускорения тела от времени.

Зависимость скорости от времени - это линейная функция, графиком которой является прямая линия (рис. 1.16).

Рис. 1.16. Зависимость скорости тела от времени.

График зависимости скорости от времени (рис. 1.16) показывает, что

При этом перемещение численно равно площади фигуры 0abc (рис. 1.16).

Площадь трапеции равна произведению полусуммы длин её оснований на высоту. Основания трапеции 0abc численно равны:

0a = v0 bc = v

Высота трапеции равна t. Таким образом, площадь трапеции, а значит, и проекция перемещения на ось ОХ равна:

В случае равнозамедленного движения проекция ускорения отрицательна и в формуле для проекции перемещения перед ускорением ставится знак «-» (минус).

График зависимости скорости тела от времени при различных ускорениях показан на рис. 1.17. График зависимости перемещения от времени при v0 = 0 показан на рис. 1.18.

Рис. 1.17. Зависимость скорости тела от времени для различных значений ускорения.

Рис. 1.18. Зависимость перемещения тела от времени.

Скорость тела в данный момент времени t 1 равна тангенсу угла наклона между касательной к графику и осью времени v = tg α, а перемещение определяют по формуле:

Если время движения тела неизвестно, можно использовать другую формулу перемещения, решая систему из двух уравнений:

Поможет нам вывести формулу для проекции перемещения:

Так как координата тела в любой момент времени определяется суммой начальной координаты и проекции перемещения, то будет выглядеть следующим образом:

Графиком координаты x(t) также является парабола (как и график перемещения), но вершина параболы в общем случае не совпадает с началом координат. При а x < 0 и х 0 = 0 ветви параболы направлены вниз (рис. 1.18).

Равномерное движение – это движение с постоянной скоростью, то есть когда скорость не изменяется (v = const) и ускорения или замедления не происходит (а = 0).

Прямолинейное движение – это движение по прямой линии, то есть траектория прямолинейного движения – это прямая линия.

Равномерное прямолинейное движение – это движение, при котором тело за любые равные промежутки времени совершает одинаковые перемещения. Например, если мы разобьём какой-то временной интервал на отрезки по одной секунде, то при равномерном движении тело будет перемещаться на одинаковое расстояние за каждый из этих отрезков времени.

V cp = v

V x = v, то есть v > 0

Проекция перемещения на ось ОХ равна:

S = vt = x – x 0

где x 0 – начальная координата тела, х – конечная координата тела (или координата тела в любой момент времени)

Уравнение движения , то есть зависимость координаты тела от времени х = х(t), принимает вид:

Х = x 0 + vt

Х = x 0 - vt

Зависимость скорости, координат и пути от времени

Зависимость проекции скорости тела от времени показана на рис. 1.11. Так как скорость постоянна (v = const), то графиком скорости является прямая линия, параллельная оси времени Ot.

Рис. 1.11. Зависимость проекции скорости тела от времени при равномерном прямолинейном движении.

Проекция перемещения на координатную ось численно равна площади прямоугольника ОАВС (рис. 1.12), так как величина вектора перемещения равна произведению вектора скорости на время, за которое было совершено перемещение.

Рис. 1.12. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

График зависимости перемещения от времени показан на рис. 1.13. Из графика видно, что проекция скорости равна

V = s 1 / t 1 = tg α

где α – угол наклона графика к оси времени.Чем больше угол α, тем быстрее движется тело, то есть тем больше его скорость (больший путь тело проходит за меньшее время). Тангенс угла наклона касательной к графику зависимости координаты от времени равен скорости:

Tg α = v

Рис. 1.13. Зависимость проекции перемещения тела от времени при равномерном прямолинейном движении.

Зависимость координаты от времени показана на рис. 1.14. Из рисунка видно, что

Tg α 1 > tg α 2

следовательно, скорость тела 1 выше скорости тела 2 (v 1 > v 2).

Tg α 3 = v 3 < 0

Если тело покоится, то графиком координаты является прямая, параллельная оси времени, то есть

Х = х 0

Рис. 1.14. Зависимость координаты тела от времени при равномерном прямолинейном движении.

Проекции скоростей двух точек твердого тела на ось, проходящую через эти точки, равны друг другу.
v A cos α = v B cos β .

Доказательство

Выберем прямоугольную неподвижную систему координат Oxyz . Возьмем две произвольные точки твердого тела A и B . Пусть (x A , y A , z A ) и (x B , y B , z B ) - координаты этих точек. При движении твердого тела они являются функциями от времени t . Дифференцируя по времени, получаем проекции скоростей точек.
, .

Воспользуемся тем, что при движении твердого тела, расстояние | AB| между точками остается постоянным, то есть не зависит от времени t . Также постоянным является квадрат расстояния
.
Продифференцируем это уравнение по времени t , применяя правило дифференцирования сложной функции.

Сократим на 2 .
(1)

Введем вектор
.
Тогда уравнение (1) можно представить в виде скалярного произведения векторов.
(2)
Выполняем преобразования.
;
(3) .
По свойству скалярного произведения
,
.
Подставляем в (3) и сокращаем на | AB| .
;

Что и требовалось доказать.

Относительная скорость

Рассмотрим движение точки B относительно точки A . Введем относительную скорость точки B относительно A .

Тогда уравнение (2) можно переписать в виде
.

То есть относительная скорость перпендикулярна вектору , проведенному из точки A в точку B . Поскольку точка B взята произвольным образом, то относительная скорость любой точки твердого тела перпендикулярна радиус вектору, проведенному из точки A . То есть относительно точки A тело совершает вращательное движение. Относительная скорость точек тела определяется по формуле для вращательного движения
.

Точку A , относительно которой рассматривают движение, часто называют полюсом .

Абсолютную скорость точки B относительно неподвижной системы координат можно записать в следующем виде:
.
Она равна сумме скорости поступательного движения произвольной точки A (полюса) и скорости вращательного движения относительно полюса A .

Пример решения задачи

Условие задачи

Колеса 1 и 2 с радиусами R 1 = 0,15 м и R 2 = 0,3 м , соответственно, соединены шарнирами со стержнем 3 длины | AB| = 0,5 м . Колесо 1 вращается с угловой скоростью ω 1 = 1 рад/с . Для изображенного на рисунке положения механизма, определить угловую скорость ω 2 колеса 2. Принять L = 0,3 м .

Решение задачи

Точка A движется по окружности радиуса R 1 вокруг центра вращения O 1 . Скорость точки A определяется по формуле
V A = ω 1 R 1 .
Вектор направлен вертикально (перпендикулярно O 1 A ).

Точка B движется по окружности радиуса R 2 вокруг центра вращения O 2 . Скорость точки B определяется по формуле
V B = ω 2 R 2 .
Отсюда
.
Вектор направлен горизонтально (перпендикулярно O 2 B ).

Строим прямоугольный треугольник ABC . Применяем теорему Пифагора.
(м)
.
Косинус угла между вектором скорости и прямой AB , в направлении вектора , равен
.

По теореме о проекциях скоростей двух точек твердого тела на прямую имеем:
V A cos α = V B cos β .
Отсюда
.

Находим угловую скорость колеса 2 .
рад/с .

Статьи по теме